从零实现高性能 CPU 矩阵乘法：逼近 OpenBLAS 的优化之路

在大模型推理引擎开发中，矩阵乘法（GEMM）是最核心的计算密集型算子。虽然可以直接调用 OpenBLAS、MKL 等成熟库，但在实际工程中存在一些问题：

1. 库体积问题：OpenBLAS 占用数十 MB，影响推理引擎的部署体积
2. 线程池冲突：OpenBLAS 内部维护线程池，与 OpenMP 混用时会产生资源竞争
3. 学习价值：手写 GEMM 是理解计算机体系结构的绝佳实践

本文记录了我从零实现一个高性能 CPU 矩阵乘法的完整过程，最终在单核条件下达到 OpenBLAS 82% 的性能，而在 24 核并行时超越 OpenBLAS 6%。具体的性能测试结果参见：https://github.com/tianyuxbear/matmul-cpu

问题定义：

所有矩阵均为 行主序(Row-Major) 存储。

测试环境：

CPU:             Intel Xeon Silver 4310 @ 2.10GHz (Turbo: 3.30GHz)
Sockets:         2
Cores/Socket:    12
Physical Cores:  24

Cache (per core):
  L1d:           48 KiB
  L2:            1.25 MiB
  L3:            18 MiB (shared)

ISA Extensions:  AVX, AVX2, AVX-512 (F/DQ/BW/VL/VNNI/VBMI/VBMI2)

理论峰值性能^[1]：

单精度峰值 FLOPS = 频率 × FMA端口数 × 每FMA操作数 × SIMD宽度
                = 2.2 GHz × 2 × 2 × 16
                = 140.8 GFLOPS/core (基频)
                = 211.2 GFLOPS/core (睿频)

理论峰值内存带宽^[1]：

理论峰值内存带宽：
= 内存传输速率 × 内存通道数 × 每通道数据宽度
= 2667 MT/s × 8 × 8 Byte
≈ 170.7 GB/s（单 Socket, 12核共享）
≈ 341.4 GB/s（双 Socket）

最终性能：

矩阵规模 M = N = K = 4096，2 次预热（warmup）轮次，10 次正式基准测试（benchmark）轮次。

配置	实现	Peak GFLOPS	Avg GFLOPS	vs OpenBLAS
单核	本文实现	110.74	109.37	82.4%
单核	OpenBLAS	132.88	132.62	—
24核	本文实现	2010.61	1909.40	106%
24核	OpenBLAS	1914.91	1796.69	—

第一部分：理论基础

1.1 Roofline 模型：计算瓶颈 vs 访存瓶颈

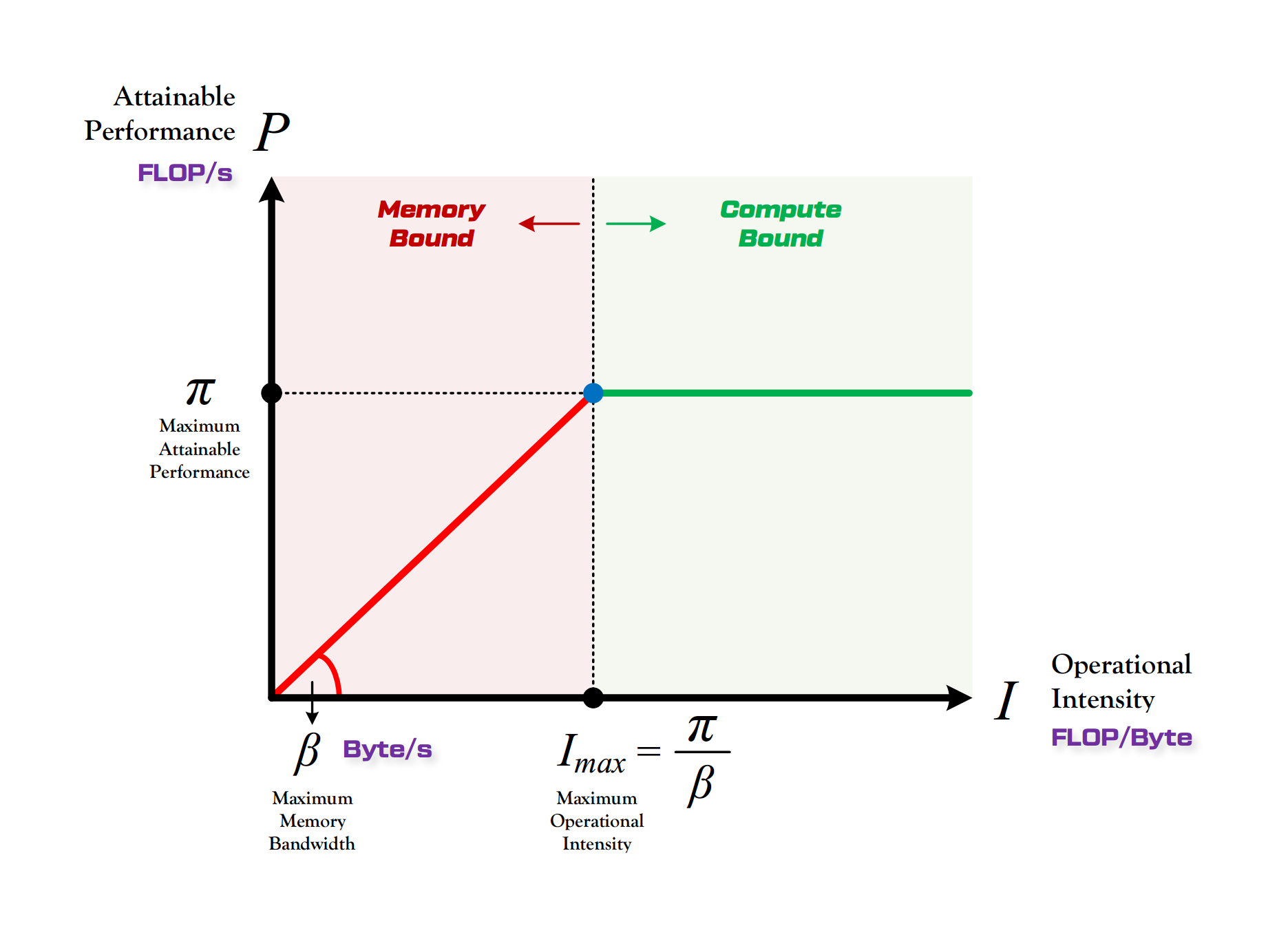
• 算力 π：也称为计算平台的性能上限，指的是一个计算平台倾尽全力每秒钟所能完成的浮点运算数。单位是 FLOPS 或 FLOP/s^[2]。

• 带宽 β：也即计算平台的带宽上限，指的是一个计算平台倾尽全力每秒所能完成的内存交换量。单位是 Byte/s^[2]。

• 计算强度上限 I_max：两个指标相除即可得到计算平台的计算强度上限。它描述的是在这个计算平台上，单位内存交换最多用来进行多少次计算。单位是 FLOPs/Byte^[2]。

注：这里所说的“内存”是广义上的内存。对于 CPU 计算平台而言指的就是真正的内存；而对于 GPU 计算平台指的则是显存^[2]。

1.2 对朴素实现的观察

/* Naive reference implementation for correctness testing (single-threaded)
 * Operation: C = A * B^T + C
 * * Dimensions:
 * C: [M, N]
 * A: [M, K]
 * B: [N, K]
 * * Layout:
 * Matrices A, B, and C are stored in row-major order.
 */
void matmul_ref(const float *A, const float *B, float *C, size_t M, size_t N, size_t K) {
    for (size_t i = 0; i < M; ++i) {
        for (size_t j = 0; j < N; ++j) {
            float sum = 0.0f;
            for (size_t k = 0; k < K; ++k) {
                // A[i][k] * B[j][k] (Accessing B as N*K row-major)
                sum += A[i * K + k] * B[j * K + k];
            }
            C[i * N + j] += sum;
        }
    }
}

计算量与访存量分析：

对于 C[M, N] 中每一个元素 C[i,j] 的计算：
  • 需要读取：A[i, 0:K]（K 个元素）+ B[j, 0:K]（K 个元素）
  • 需要计算：K 次乘法 + K 次加法

总计算量 = M × N × 2K = 2MNK FLOPs

总访存量（最坏情况，无缓存复用）：
  • 读取 A：每个 C[i,j] 读取 K 个 float = M × N × K × 4 bytes
  • 读取 B：每个 C[i,j] 读取 K 个 float = M × N × K × 4 bytes  
  • 写入 C：M × N × 4 bytes
  = (2MNK + MN) × 4 bytes ≈ 8MNK bytes

计算访存比 = 2MNK / 8MNK = 0.25 FLOPs/Byte

与 Roofline 拐点对比：

内存带宽 ≈ 170 GB/s（DDR4 双通道）
计算峰值 ≈ 140 GFLOPS（单核基频）

Roofline 拐点 = 140 / 170 = 0.82 FLOPs/Byte

朴素实现：0.25 FLOPs/Byte < 0.82 FLOPs/Byte
→ 处于 Memory Bound 区域

问题总结：

问题	原因	影响
计算访存比极低	无数据复用，每个元素重复加载	受限于内存带宽
无 SIMD	标量操作	浪费 16 倍算力
无指令并行	循环依赖（C[i][j] 累加）	流水线停顿

理想情况：

优化后（理想情况，每个元素只加载一次）：
  计算量 = 2MNK（不变）
  访存量 = 读取 A + 读取 B + 读写 C
        = (MK + NK + 2MN) × 4 bytes

当 M = N = K 时：
  计算量 = 2N³
  访存量 ≈ 4 × 4N² = 16N² bytes
  
  计算访存比 = 2N³ / 16N² = N/8 FLOPs/Byte

即计算访存比与矩阵维度 N 成正比，记为 O(N)。

优化的核心目标： 通过分块和数据复用，将计算访存比从 0.25 提升到接近 O(N)，让算法从 Memory Bound 转变为 Compute Bound。

第二部分：优化策略全景

🚀 GEMM 优化技术栈演进路线

🏁 Level 0  朴素实现
   └─ 基准版本（无优化）

⚡ Level 1  SIMD 向量化（AVX2 / AVX-512）
   └─ 6 ~ 7 GFLOPS

📦 Level 2  Loop tiling（基础分块，提高局部性）
   └─ ~ 20 GFLOPS

⚙️ Level 3  多级缓存分块 + 数据打包 + 寄存器分块
   └─ ~110 GFLOPS（≈78% Peak，82% OpenBLAS）

🔥 Level 4  多线程并行（OpenMP）
   └─ ~ 1909 GFLOPS（24 核全力输出）

Level 3 优化技术：

• Multi-level cache blocking：根据 L1/L2/L3 容量设计分块参数（MC, NC, KC），精确控制数据驻留层级
• Data packing：将分块数据重排为连续内存布局，提升 cache line 利用率和预取效率
• Register blocking：设计 14×32 微内核，最大化 ZMM 寄存器复用，采用外积累加消除数据依赖

基线测试结果

Kernel	描述	Peak GFLOPS	Avg GFLOPS
core_v1_avx2	AVX2 向量化内层循环	6.42	6.35
core_v2_avx512	AVX-512 向量化内层循环	7.12	7.07
core_v3_block	简单 2D 循环分块	19.74	19.73

注意：AVX-512 相比 AVX2 提升很小，因为此时内核是访存瓶颈——单纯增加计算吞吐而不优化内存访问模式，收益微乎其微。

源码链接

• core_v1_avx2: https://github.com/tianyuxbear/matmul-cpu/blob/master/src/core/matmul_v1_av2.cpp
• core_v2_avx512: https://github.com/tianyuxbear/matmul-cpu/blob/master/src/core/matmul_v2_avx512.cpp
• core_v3_block: https://github.com/tianyuxbear/matmul-cpu/blob/master/src/core/matmul_v3_avx512_block.cpp

• SIMD向量化一条指令可以处理 8/16 个float，提高了计算吞吐。
• 基础分块提升局部性的本质：通过减小工作集大小，让数据驻留在更快的缓存层级中，被多次复用后再换出。

第三部分：基础分块优势

3.1 朴素版本的问题

// 假设 M=1024, N=1024, K=1024
for (int i = 0; i < M; i++) {       // 1024 次
    for (int j = 0; j < N; j++) {   // 1024 次
        dot_product(A[i], B[j]);    // 每次读取 K=1024 个元素
    }
}

内存访问分析：

矩阵	每次内循环读取	总读取次数	总数据量
A[i]	K 个元素	M × N 次	M × N × K
B[j]	K 个元素	M × N 次	M × N × K

问题所在：

外循环 i=0 时：
  j=0: 读 A[0], B[0]
  j=1: 读 A[0], B[1]    ← A[0] 重复读取，但 B 在快速变化
  j=2: 读 A[0], B[2]
  ...
  j=1023: 读 A[0], B[1023]
  
外循环 i=1 时：
  j=0: 读 A[1], B[0]    ← B[0] 又要重新读！之前早被踢出缓存了
  j=1: 读 A[1], B[1]

B 矩阵的每一行被读取了 M 次，但由于 B 太大无法全部放入缓存，每次都要从主存重新加载！

3.2 分块版本的优势

// 完整的分块矩阵乘法
#define TILE 16

for (int i0 = 0; i0 < M; i0 += TILE) {           // 遍历 A 的行块
    for (int j0 = 0; j0 < N; j0 += TILE) {       // 遍历 B 的行块
        // 处理 C[i0:i0+TILE, j0:j0+TILE] 这个子块
        for (int i = i0; i < i0 + TILE; i++) {
            for (int j = j0; j < j0 + TILE; j++) {
                C[i][j] = dot_product(A[i], B[j]);
            }
        }
    }
}

假设：M=N=K=1024，TILE=16，每个元素 4 字节

朴素版本内存访问：

处理整个矩阵：

• A 总读取：M × N × K × 4 bytes = 1024 × 1024 × 1024 × 4 = 4 GB
• B 总读取：M × N × K × 4 bytes = 4 GB
• 总计：8 GB 数据传输

分块版本内存访问：

处理一个 16×16 的 C 子块：

• 需要 A 的 16 行：16 × 1024 × 4 = 64 KB
• 需要 B 的 16 行：16 × 1024 × 4 = 64 KB
• 这 128 KB 可以放入 L2 Cache！

整个矩阵有 (1024/16) × (1024/16) = 4096 个子块

• A 的每行被读取 1024/16 = 64 次（分布在 64 个列方向的子块中）
• B 的每行被读取 1024/16 = 64 次（分布在 64 个行方向的子块中）

总数据传输：

• A：M × K × (N/TILE) × 4 = 1024 × 1024 × 64 × 4 = 256 MB
• B：N × K × (M/TILE) × 4 = 256 MB
• 总计：512 MB

相比朴素版本的 8 GB，减少了 16 倍！（恰好等于 TILE 大小）

图示理解

朴素版本：缓存不断被刷新
═══════════════════════════════════════

时间 t1: Cache = [A[0], B[0], B[1], B[2]...]
时间 t2: Cache = [A[0], B[100], B[101]...]  ← B[0-99] 被踢出
时间 t3: Cache = [A[1], B[0], B[1]...]      ← 需要重新加载 B[0]！
                  ↑ 
                  A[0] 也被踢出了

分块版本：数据留在缓存中被反复使用
═══════════════════════════════════════

处理子块 (0,0):
Cache = [A[0:16], B[0:16]]  ← 加载一次
        ↓
        16×16=256 次点积全部命中缓存！
        
处理子块 (0,1):
Cache = [A[0:16], B[16:32]]  ← A[0:16] 已在缓存！只需加载新的 B

分块的三大优势

优势	说明
1. 缓存命中率↑	小块数据能放入缓存，反复使用不被踢出
2. 内存带宽需求↓	总数据传输量降低 TILE 倍
3. 计算访存比↑	同样的数据量产生更多计算，更接近硬件算力峰值

在 GPU 上，分块更加关键——因为 GPU 有专门的 Shared Memory（共享内存），分块可以让数据从慢速的 Global Memory 加载到快速的 Shared Memory，大幅提升性能。这正是 CUDA 矩阵乘法优化的核心思想。

第四部分：寄存器分块——微内核设计

阅读本文以下内容前，请务必通读参考链接3^[3]的文章内容，对计算内核的外积计算方式以及缓存分块技术有一定了解。

4.1 寄存器资源分析

AVX-512 提供 32 个 512-bit 的 ZMM 寄存器，每个可存储 16 个 float。微内核（micro-kernel）的目标是最大化寄存器利用率，让尽可能多的数据驻留在寄存器中。

4.2 分块尺寸推导

设微内核计算 C 的一个 MR × NR 子块：

寄存器分配：
- C 累加器：MR × (NR / 16) 个 ZMM
- A 广播寄存器：1 个 ZMM
- B 数据寄存器：NR / 16 个 ZMM
- 临时寄存器：≥ 1 个

约束条件：

注：因为本文是基于行主序实现，所以要求一定是16的整数倍，便于写入分块的 C[MR, NR]。

两种可行配置：

配置	C 寄存器	A	B	临时	总计	每迭代 FMA
MR=30, NR=16	30	1	1	0	32	30
MR=14, NR=32	28	1	2	1	32	28

4.3 为什么选择 MR=14, NR=32？

虽然 30×16 配置的 FMA 数量更多，但实测 14×32 性能更优，原因如下：

a. 端口竞争分析

每次 K 迭代的指令分布：

配置 30×16：

• Broadcast: 30 次 → Port 5，需要 30 cycles
• FMA: 30 次 → Port 0/1，需要 15 cycles
• Load: 1 次 → Port 2/3，需要 0.5 cycle

→ Port 5 成为瓶颈！

配置 14×32：

• Broadcast: 14 次 → Port 5，需要 14 cycles
• FMA: 28 次 → Port 0/1，需要 14 cycles
• Load: 2 次 → Port 2/3，需要 1 cycle

→ FMA 和 Broadcast 平衡！

注：此部分为claude的分析结果，Broadcast、FMA、Load的计算次数是正确的，Inst Issue Port和Latency尚未查证。

b. Cache Line 利用率

14×32 配置：

• B 每次加载 32 float = 128 bytes = 2 个完整 cache line ✓

30×16 配置：

• B 每次加载 16 float = 64 bytes = 1 个 cache line ✓
• 但 A 需要 30 float = 120 bytes，跨 2 个 cache line，可能有浪费

4.4 微内核代码实现

/**
 * @brief The Core FMA Loop.
 * Computes 14x32 block dot product over the K-dimension (size kc).
 * Uses explicit loop unrolling for maximum pipeline utilization.
 */
static inline void fma_loop(float *packedA, float *packedB,
                            __m512 C_accum[MR][2],
                            __m512 *va, __m512 *vb0, __m512 *vb1, int kc) {

    for (int k = 0; k < kc; ++k) {
        // Load 32 elements of B (2 ZMMs)
        // Since B is packed, these are sequential loads.
        *vb0 = _mm512_loadu_ps(packedB);
        *vb1 = _mm512_loadu_ps(packedB + 16);

// Broadcast A elements and multiply-add
// Unrolling MR (14) times
#define UNROLL_FMA(i)                                          \
    *va = _mm512_set1_ps(packedA[i]);                          \
    C_accum[i][0] = _mm512_fmadd_ps(*va, *vb0, C_accum[i][0]); \
    C_accum[i][1] = _mm512_fmadd_ps(*va, *vb1, C_accum[i][1]);

        UNROLL_FMA(0);
        UNROLL_FMA(1);
        UNROLL_FMA(2);
        UNROLL_FMA(3);
        UNROLL_FMA(4);
        UNROLL_FMA(5);
        UNROLL_FMA(6);
        UNROLL_FMA(7);
        UNROLL_FMA(8);
        UNROLL_FMA(9);
        UNROLL_FMA(10);
        UNROLL_FMA(11);
        UNROLL_FMA(12);
        UNROLL_FMA(13);

#undef UNROLL_FMA

        // Advance pointers
        // A moves by MR (14 floats), B moves by NR (32 floats)
        packedA += MR;
        packedB += NR;
    }
}

/**
 * @brief The Micro-Kernel.
 * Manages register allocation, accumulation, and boundary masking.
 */
static inline void micro_kernel(float *packedA, float *packedB, float *C,
                                int mr, int nr, int kc, int N_stride) {

    __m512 C_accum[MR][2];        // 28 Registers used for Accumulation
    __m512 a_reg, b0_reg, b1_reg; // 3 Registers for operands
    // Total regs used: ~31 (fits in 32 ZMMs)

    if (likely(nr == NR)) {
        load_accum(C, C_accum, N_stride, mr);
        fma_loop(packedA, packedB, C_accum, &a_reg, &b0_reg, &b1_reg, kc);
        store_accum(C, C_accum, N_stride, mr);
    } else {
        // Boundary handling with masks
        __mmask16 mask0 = create_mask(nr);
        __mmask16 mask1 = create_mask(nr - 16);

        maskload_accum(C, C_accum, N_stride, mr, mask0, mask1);
        fma_loop(packedA, packedB, C_accum, &a_reg, &b0_reg, &b1_reg, kc);
        maskstore_accum(C, C_accum, N_stride, mr, mask0, mask1);
    }
}

4.5 外积（Rank-1 Update）的数学本质

矩阵乘法可以分解为 K 次 Rank-1 Update：

其中 ⊗ 表示外积：

外积相比内积的优势：

方面	内积	外积
累加器数量	1 个（当前 C[i,j]）	MR × NR 个（整个子块）
累加器位置	频繁换入换出内存	全程驻留寄存器
单次迭代	计算 1 个 C 元素	更新 448 个 C 元素
A 的复用	被 N 个 B 行复用（跨时间）	被 NR 个 B 元素复用（同时）
B 的复用	无（每个 B 行只用一次）	被 MR 个 A 元素复用（同时）

关键区别： 内积的复用是”跨时间”的（A 行在计算多个 C 元素时被复用，但中间可能被换出 cache），外积的复用是”同时”的（A 和 B 在同一批指令中互相复用，数据就在寄存器里）。

第五部分：缓存分块——多级存储层次优化

BLIS设计示意图:

记得回忆一下参考链接3^[3]中的缓存分块内容。

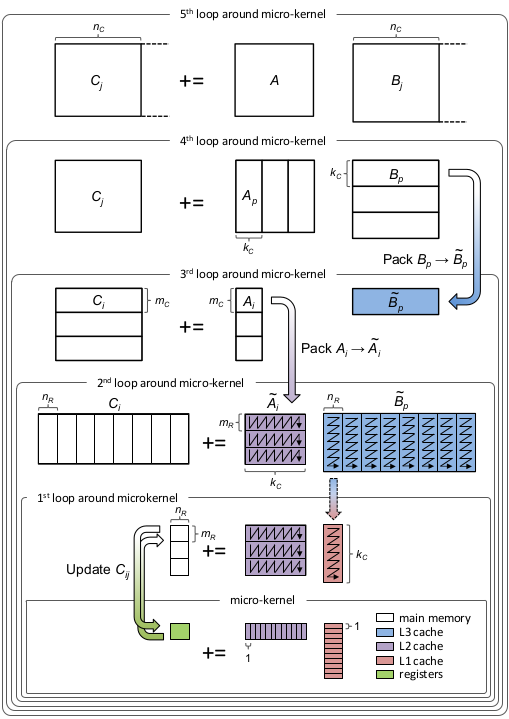
5.1 缓存层次与数据块大小

/*
 * ┌──────────────────────────────────────────────────────────────────────┐
 * │  Goal: Maximize data reuse before eviction (Tiling Strategy)         │
 * ├─────────────┬──────────────┬──────────────────┬──────────────────────┤
 * │ Cache Level │ Capacity     │ Data Block       │ Reuse Strategy       │
 * ├─────────────┼──────────────┼──────────────────┼──────────────────────┤
 * │ L1 (48KB)   │ Smallest/    │ A[MR, KC]        │ Inside Micro-kernel  │
 * │             │ Fastest      │ B[NR, KC]        │ Reuse: KC times      │
 * ├─────────────┼──────────────┼──────────────────┼──────────────────────┤
 * │ L2 (1.25MB) │ Medium       │ A[MC, KC]        │ Inside jr loop       │
 * │             │              │                  │ Reuse: NC/NR times   │
 * ├─────────────┼──────────────┼──────────────────┼──────────────────────┤
 * │ L3 (18MB)   │ Largest/     │ B[NC, KC]        │ Inside i loop        │
 * │             │ Slowest      │                  │ Reuse: M/MC times    │
 * └─────────────┴──────────────┴──────────────────┴──────────────────────┘
 */

5.2 分块参数计算

根据缓存大小反推分块参数：

约束条件：

• KC × NR × 4 ≤ L1_size (B panel 放 L1)
• MC × KC × 4 ≤ L2_size (A block 放 L2)
• NC × KC × 4 ≤ L3_size (B block 放 L3)

对于配置 MR=14, NR=32：

• KC = 384（保证 B panel 适合 L1）
• MC = 840（保证 A block 适合 L2）
• NC = 1024（保证 B block 适合 L3）

claude insight

/*
 * ============================================================
 * [ L1 Cache Budget Analysis ] Total: 48 KB
 * ============================================================
 *
 * 1. Resident Block (B Panel):
 * -------------------------
 * Dim : NR(32) x KC(384)
 * Size: 48 KB
 * Note: TAKES 100% ROOM. No space left for A.
 *
 * 2. Streaming Block (A Panel):
 * --------------------------
 * Dim : MR(14) x KC(384)
 * Size: 21 KB
 * Note: CACHE SPILL. Performance penalty.
 *
 * ------------------------------------------------------------
 * TOTAL REQUIRED: ~69 KB  ( > 48 KB Limit )
 * ACTION: Reduce KC block size.
 * ============================================================
 */

claude 认为前面的约束条件中：

• KC × NR × 4 ≤ L1_size / 2 (B panel 放 L1)

是比较好的工程实践，原因如下：

1. A 的访问：虽然 A 主要驻留 L2，但当前 micro-kernel 正在使用的 A[MR, KC] 也会进入 L1
2. 避免 cache 颠簸：如果 B panel 占满 L1，A 的访问会把 B 换出，然后 B 又把 A 换出，反复颠簸
3. 安全余量：L1 cache 是组相联的，不是所有空间都能被有效利用，预留一半是工程经验值

简单来说： 除以 2 是为了给 A 和其他数据留出空间，避免 B 和 A 在 L1 中互相驱逐。

5.3 循环嵌套结构

// Optimization: Cache Blocking + Packing + Register Blocking (AVX-512)
// C = A * B^T + C
// Layout: C[M, N], A[M, K], B[N, K] (Row-Major)
void matmul_v4_cache_opt(const float *A, const float *B, float *C, size_t M, size_t N, size_t K) {

    // 1. Loop over N (L3 Cache Blocking for B)
    for (size_t j = 0; j < N; j += NC) {
        int nc = MIN(N - j, NC);

        // 2. Loop over K (Reduction Dimension)
        for (size_t p = 0; p < K; p += KC) {
            int kc = MIN(K - p, KC);

            // Pack Block B into contiguous memory (L2 Cache friendly)
            pack_blockB(&B[j * K + p], blockB_packed, nc, kc, K);

            // 3. Loop over M (L2 Cache Blocking for A)
            for (size_t i = 0; i < M; i += MC) {
                int mc = MIN(M - i, MC);

                // Pack Block A into contiguous memory
                pack_blockA(&A[i * K + p], blockA_packed, mc, kc, K);

                // 4. Micro-Kernel Loops (Register Blocking)
                // Iterate over the packed blocks
                for (int jr = 0; jr < nc; jr += NR) {
                    int nr = MIN(NR, nc - jr);

                    for (int ir = 0; ir < mc; ir += MR) {
                        int mr = MIN(MR, mc - ir);

                        // Compute 14x32 block
                        micro_kernel(
                            &blockA_packed[ir * kc], // A ptr moves by KC * MR elements
                            &blockB_packed[jr * kc], // B ptr moves by KC * NR elements
                            &C[(i + ir) * N + (j + jr)],
                            mr, nr, kc, N);
                    }
                }
            }
        }
    }
}

5.4 数据复用分析

B[NC, KC] 的复用：
─────────────────
- Pack 一次
- 在 Loop 3（i 循环）中被复用 M/MC 次
- 每个 micro-kernel 再复用 KC 次

A[MC, KC] 的复用：
─────────────────
- Pack 一次  
- 在 Loop 4（jr 循环）中被复用 NC/NR 次
- 每个 micro-kernel 再复用 KC 次

总复用率 = O(MNK) 计算量 / O(MK + NK) 访存量 ≈ O(N)

第六部分：数据打包（Packing）

6.1 为什么需要 Pack？

原始 B[N, K] 按行存储：

内存地址: [B00 B01 B02 ... B0,K-1] [B10 B11 B12 ... B1,K-1] ...

micro-kernel 需要读取 B[:, k]（一列）：
  B[0,k], B[1,k], B[2,k], ..., B[31,k]
  地址跨度 = K × sizeof(float)

问题：
  • 如果 K=4096，每次跨越 16KB！
  • Cache line 利用率 = 1/K ≈ 0
  • 预取器无法预测访问模式

6.2 Pack 后的内存布局

Pack B 后的布局（按 k 优先）：

┌─────────────────────────────────────────────────────────────┐
│ B[0,0] B[1,0] B[2,0] ... B[31,0] │ B[0,1] B[1,1] ... B[31,1]│ ...
└─────────────────────────────────────────────────────────────┘
  └────── k=0 的 32 个元素 ──────┘   └────── k=1 的 32 个 ────┘

micro-kernel 访问 B[:, k]：
  连续读取 32 个 float = 128 bytes = 2 个 cache line ✓
  预取器可以完美预测 ✓

6.3 Pack 实现

/**
 * @brief Packs a panel of Matrix A into contiguous memory.
 * Layout: [KC, MR] (Row-Major within the block).
 * Goal:   Optimized for broadcasting A elements in the FMA loop.
 */
static inline void pack_panelA(const float *A, float *packed_ptr, int mr, int kc, int K_stride) {
    for (int k = 0; k < kc; ++k) {
        for (int i = 0; i < mr; ++i) {
            *packed_ptr++ = A[i * K_stride + k];
        }
        // Zero-padding if mr < MR
        for (int i = mr; i < MR; ++i) {
            *packed_ptr++ = 0.0f;
        }
    }
}

/**
 * @brief Block-level wrapper for packing A.
 */
static inline void pack_blockA(const float *A, float *packed_buffer, int mc, int kc, int K_stride) {
    for (int i = 0; i < mc; i += MR) {
        int mr = MIN(MR, mc - i);
        pack_panelA(&A[i * K_stride], &packed_buffer[i * kc], mr, kc, K_stride);
    }
}

/**
 * @brief Packs a panel of Matrix B into contiguous memory.
 * Layout: [KC, NR] (Row-Major within the block).
 * Goal:   Optimized for sequential vector loads (ZMM) in the FMA loop.
 */
static inline void pack_panelB(const float *B, float *packed_ptr, int nr, int kc, int K_stride) {
    for (int k = 0; k < kc; ++k) {
        for (int j = 0; j < nr; ++j) {
            *packed_ptr++ = B[j * K_stride + k];
        }
        // Zero-padding if nr < NR
        for (int j = nr; j < NR; ++j) {
            *packed_ptr++ = 0.0f;
        }
    }
}

/**
 * @brief Block-level wrapper for packing B.
 */
static inline void pack_blockB(const float *B, float *packed_buffer, int nc, int kc, int K_stride) {
    for (int j = 0; j < nc; j += NR) {
        int nr = MIN(NR, nc - j);
        pack_panelB(&B[j * K_stride], &packed_buffer[j * kc], nr, kc, K_stride);
    }
}

6.4 Pack 开销分析

Pack 开销 = O(MK + NK)
计算开销 = O(MNK)

比例 = (MK + NK) / (MNK) = 1/N + 1/M

当 M = N = K = 4096 时：
  Pack 占比 ≈ 2/4096 ≈ 0.05%

结论：对于大矩阵，Pack 开销可以忽略不计

第七部分：指令级并行与循环展开

7.1 FMA 指令的流水线特性

Intel Skylake-X / Ice Lake 的 FMA 特性：
  • Latency（延迟）: 4 cycles
  • Throughput（吞吐）: 2/cycle（Port 0 和 Port 1）

要打满吞吐，需要足够的独立指令填充流水线：
  所需独立 FMA 数 = Latency × Throughput = 4 × 2 = 8

7.2 FMA 循环展开

1. 消除循环控制开销

// 未展开：每次迭代有额外开销
for (int i = 0; i < 14; ++i) {
    C[i] = FMA(A[i], B, C[i]);
    // 隐含：i++, cmp i < 14, jmp
}

// 展开后：纯计算，无控制指令
C[0] = FMA(A[0], B, C[0]);
C[1] = FMA(A[1], B, C[1]);
...

2. 帮助编译器优化寄存器分配

// 未展开：编译器可能通过内存/索引访问 C[i]
C[i] = ...  // i 是变量，可能无法确定分配哪个寄存器

// 展开后：编译器明确知道每个累加器，直接分配到固定寄存器
C_accum_0 = ...  // → ZMM0
C_accum_1 = ...  // → ZMM1
...

3. 增加指令级并行的可见性
   虽然 C[0]~C[13] 本身独立，但展开后 CPU 的调度器能更容易地同时发射多条独立指令，而不需要动态分析循环迭代间的独立性。

第八部分：多线程并行化

8.1 并行策略

constexpr int NTHREADS = 24;

// Helper to stringify the thread count for the pragma
#define PRAGMA_STR(x) _Pragma(#x)

// We strictly enforce num_threads to match our blocking logic.
// Usage: PARALLEL_FOR_LOOP
#define PARALLEL_FOR_LOOP PRAGMA_STR(omp parallel for num_threads(NTHREADS))

/**
 * @brief Packs a block of Matrix A in PARALLEL.
 * Splitting the packing workload speeds up the pre-processing phase.
 */
static inline void pack_blockA(const float *A, float *packed_buffer, int mc, int kc, int K_stride) {
    PARALLEL_FOR_LOOP
    for (int i = 0; i < mc; i += MR) {
        int mr = MIN(MR, mc - i);
        // Each thread packs a distinct panel, no data race on packed_buffer.
        pack_panelA(&A[i * K_stride], &packed_buffer[i * kc], mr, kc, K_stride);
    }
}

/**
 * @brief Packs a block of Matrix B in PARALLEL.
 */
static inline void pack_blockB(const float *B, float *packed_buffer, int nc, int kc, int K_stride) {
    PARALLEL_FOR_LOOP
    for (int j = 0; j < nc; j += NR) {
        int nr = MIN(NR, nc - j);
        pack_panelB(&B[j * K_stride], &packed_buffer[j * kc], nr, kc, K_stride);
    }
}

// Optimization: Cache Blocking + Packing + Register Blocking + OpenMP Parallelism
// C = A * B^T + C
// Layout: Row-Major
void matmul_v5_parallel(const float *A, const float *B, float *C, size_t M, size_t N, size_t K) {

    // 1. Loop over N (L3 Cache Blocking for B)
    for (size_t j = 0; j < N; j += NC) {
        int nc = MIN(N - j, NC);

        // 2. Loop over K (Reduction Dimension)
        for (size_t p = 0; p < K; p += KC) {
            int kc = MIN(K - p, KC);

            // Pack B in PARALLEL
            // Threads work on disjoint parts of blockB_packed -> Thread Safe.
            pack_blockB(&B[j * K + p], blockB_packed, nc, kc, K);

            // 3. Loop over M (L2 Cache Blocking for A)
            for (size_t i = 0; i < M; i += MC) {
                int mc = MIN(M - i, MC);

                // Pack A in PARALLEL
                // Threads work on disjoint parts of blockA_packed -> Thread Safe.
                pack_blockA(&A[i * K + p], blockA_packed, mc, kc, K);

                // 4. Parallel Compute Loop
                // Threads divide the columns (jr) of the current block.
                // All threads read from the shared blockA_packed and blockB_packed (Read-Only).
                // Threads write to disjoint parts of C (Write-Safe).
                PARALLEL_FOR_LOOP
                for (int jr = 0; jr < nc; jr += NR) {
                    int nr = MIN(NR, nc - jr);

                    for (int ir = 0; ir < mc; ir += MR) {
                        int mr = MIN(MR, mc - ir);

                        micro_kernel(
                            &blockA_packed[ir * kc],
                            &blockB_packed[jr * kc],
                            &C[(i + ir) * N + (j + jr)],
                            mr, nr, kc, N);
                    }
                }
            }
        }
    }
}

8.2 多核性能结果

测试配置：M = N = K = 4096，24 线程

Kernel	Peak GFLOPS	Avg GFLOPS
core_v5_parallel	2010.61	1909.40
blas_row_AB^T	1914.91	1796.69

参考资料

1. https://www.intel.com/content/www/us/en/products/sku/215277/intel-xeon-silver-4310-processor-18m-cache-2-10-ghz/specifications.html ↩
2. Roofline Model与深度学习模型的性能分析 ↩
3. 现代多核处理器上的高级矩阵乘法优化 ↩